聊聊SAT问题是什么

问题背景

SAT问题又称命题逻辑公式的可满足性问题（satisfiability problem），是判断对合取范式形式给出的命题逻辑公式是否存在一个真值指派使得该逻辑公式为真。SAT问题是计算机科学与人工智能基本问题，是一个典型的NP完全问题。看似简单，却可广泛应用于许多实际问题如人工智能、电子设计自动化、自动化推理、硬件设计、安全协议验证等，具有重要理论意义与应用价值。对于SAT问题的研究从没有停止过，在1997年和2003年，H.Kautz与B.Selman两次列举出SAT搜索面临的挑战性问题，并于2011年和2007年，两度对当时的SAT问题研究现状进行了全面的综述。黄文奇提出的Solar算法在北京第三届SAT问题快速算法比赛中获得第一名。对SAT问题的求解主要有完备算法和不完备算法两大类。不完备算法主要是局部搜索算法，这种算法不能保证一定找到解，但是求解速度快，对于某些SAT问题的求解，局部搜索算法要比很多完备算法更有效。完备算法出现的时间更早，优点是可以正确判断SAT问题的可满足性，在算例无解的情况下可以给出完备的证明。对于求解SAT问题的优化算法主要有启发式算法、冲突子句学习算法、双文字监视法等。

研究意义

SAT问题是第一个被证明的NP完全问题，而NP完全问题由于其极大的理论价值和困难程度，破解后将会在许多领域得到广泛应用，从而在计算复杂性理论中具有非常重要的地位。由于所有的NP完全问题都能够在多项式时间内进行转换，那么如果SAT问题能够得到高效解决，所有的NP完全问题都能够在多项式时间内得到解决。对SAT问题的求解，可用于解决计算机和人工智能领域内的CSP问题（约束满足问题）、语义信息的处理和逻辑编程等问题，也可用于解决计算机辅助设计领域中的任务规划与设计、三维物体识别等问题。SAT问题的应用领域非常广泛，还能用于解决数学研究和应用领域中的旅行商问题和逻辑算数问题。许多实际问题，例如数据库检索、积木世界规划、超大规模集成电路设计、人工智能等都可以转换成SAT问题进而进行求解。可见对SAT问题求解的研究，具有重大意义。

问题描述

SAT问题即命题逻辑公式的可满足性问题（satisfiability problem），是计算机科学与人工智能基本问题，是一个典型的NP完全问题，可广泛应用于许多实际问题如硬件设计、安全协议验证等，具有重要理论意义与应用价值。SAT问题也是程序设计与竞赛的经典问题。
对于任一布尔变元x，x与其非“¬x”称为文字(literal)。对于多个布尔变元，若干个文字的或运算l1∨l2∨…∨lk称为子句(clause)。只含一个文字的子句称为单子句。不含任何文字的子句称为空子句，常用符号□表示。子句所含文字越多，越易满足，空子句不可满足。
SAT问题一般可描述为：给定布尔变元集合{x1, x2, …, xn}以及相应的子句集合{c1, c2, …, cm}，对于合取范式（CNF范式）：F = c1∧c2∧…∧cm，判定是否存在对每个布尔变元的一组真值赋值使F为真，当为真时（问题是可满足的，SAT），输出对应的变元赋值（一组解）结果。
一个CNF公式也可以表示成子句集合的形式：S={c1,c2,…,cm}.
例如，由三个布尔变元a,b,c所形成的一个CNF公式（¬a∨b）∧（¬b∨c）,可用集合表示为{¬a∨b,¬b∨c}，该公式是满足的，a=0, b=0,c=1是其一组解。

cnf文件解读

一个CNF SAT公式或算例的具体信息通常存储在一个.cnf文件中，下图是算例problem1.cnf文件前若干行的截图。

在每个CNF文件的开始，由‘c’开头的是若干注释说明行；‘p’开头的行说明公式的总体信息，包括：范式为CNF；公式有200个布尔变元，由1到200的整数表示；320个子句。之后每行对应一个子句，0为结束标记。46表示第46号变元，且为正文字；-46则是对应的负文字，文字之间以空格分隔。

DPLL算法是经典的SAT完备型求解算法，对给定的一个SAT问题实例，理论上可判定其是否满足，满足时可给出对应的一组解。

DPLL算法是什么呢

DPLL算法是基于树/二叉树的回溯搜索算法，主要使用两种基本处理策略：

单子句规则。如果子句集S中有一个单子句L,那么L一定取真值，于是可以从S中删除所有包含L的子句（包括单子句本身），得到子句集S1，如果它是空集，则S可满足。否则对S1中的每个子句，如果它包含文字¬L,则从该子句中去掉这个文字，这样可得到子句集合S2。S可满足当且仅当S2可满足。单子句传播策略就是反复利用单子句规则化简S的过程。

分裂策略。按某种策略选取一个文字L.如果L取真值，则根据单子句传播策略，可将S化成S2；若L取假值（即¬L成立）时，S可化成S1.

交错使用上述两种策略可不断地对公式化简，并最终达到终止状态，其执行过程可表示为一棵二叉搜索树,如下图所示。

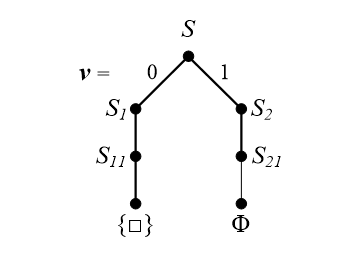
基于单子句传播与分裂策略的DPLL算法可以描述为一个如后所示的递归过程DPLL( S ), DPLL算法也可用非递归实现。

DPLL( S) :
/* S为公式对应的子句集。若其满足，返回TURE；否则返回FALSE. */
{
while(S中存在单子句) {//单子句传播
在S中选一个单子句L；
依据单子句规则，利用L化简S；
if S = Φ return(TRUE);
else if (S中有空子句 ) return（FALSE）；
}//while
基于某种策略选取变元v；         //策略对DPLL性能影响很大
if DPLL（S ∪v ）return(TURE);  //在第一分支中搜索
return DPLL(S ∪¬v);//回溯到对v执行分支策略的初态进入另一分支
}

对于公式{¬1∨2, ¬2，¬3∨4, 3∨¬5,3∨4, 3∨5，¬2∨¬5∨6} ,大家可以利用DPLL算法进行手动推理其搜索处理及回溯过程，获得求解结果。